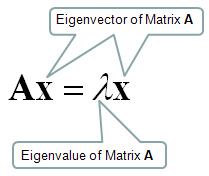|
Engineering Math - Matrix |
||
|
Eigenvector and Eigenvalue
One of the most useful/important but very hard to understand the practical meaning would be the concept of Eigenvector and Eigenvalue. You can easily find the mathematical definition of eigenvalue and eigenvector from any linear algebra books and internet surfing.
Eigen 'in Germany' means 'Characteristics' in English. So you may guess, 'Eigen vector' would be a special vector that represents a specific characteristics of a Matrix (a Square Matrix) and 'Eigen value' would be a special value that represents a specific characteristics of a Matrix (a Square Matrix)
If you think of a Matrix as a geometric transformer, the Matrix usually perform two types of transformational action. One is 'scaling(extend/shrink)' and the other one is 'rotation'. (There are some additional types of transformation like 'shear', 'reflection', but these would be described by special combination of scaling and rotation).
Eigenvector and Eigenvalue can give you the information on the scaling and rotational characteristics of a Matrix. Eigenvector would give you the rotational characteristics and Eigenvalue would give you the scaling characteristics of the Matrix. (Refer to Matrix-Geometric/Graphical Meaning of Eigenvalue and Determinant)
It means with Eigenvalue and Eigenvector, you may reasonably guess about the result of geometrical transformation of a vector without really calculalting a lot of Matrix/Vector multiplication (transformation).
Mathematical Definition of Eigenvalue
I will start with the samething, i.e mathematical definition. Mathematical definition of Eigenvalue and eigenvectors are as follows.
Let's think about the meaning of each component of this definition. I put some burbles as shown below.
When a vector is transformed by a Matrix, usually the matrix changes both direction and amplitude of the vector, but if the matrix applies to a specific vector, the matrix changes only the amplitude (magnitude) of the vector, not the direction of the vector. This specific vector that changes its amplitude only (not direction) by a matrix is called Eigenvector of the matrix.
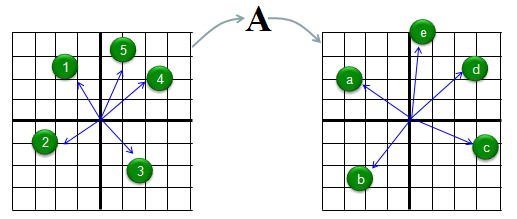
Let me try explaining the concept of eigenvector in more intuitive way. Let's assume we have a matrix called 'A'. We have 5 different vectors shown in the left side. These 5 vectors are transformed to another 5 different vectors by the matrix A as shown on the right side. Vector (1) is transformed to vector (a), Vector (2) is transformed to vector (b) and so on.
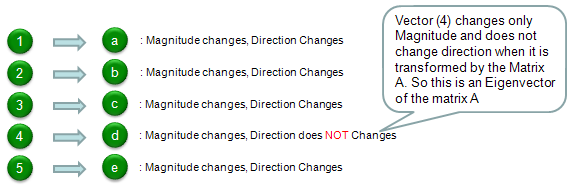
Compare the original vector and the transformed vector and check which one has changes both its direction and magnitude and which one changes its magnitude ONLY. The result in this example is as follows. According to this result, vector (4) is the eigenvector of Matrix 'A'.
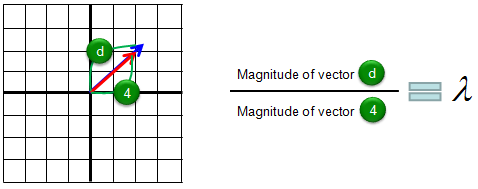
I hope you clearly understand the meaning of eigenvectors. Now we know eigenvector changes only its magnitude when applied by the corresponding matrix. Then the question is "How much in magnitude it changes ?". Did it get larger ? or smaller ? exactly how much ? The indicator showing the magnitude change is called Eigenvalue. For example, if the eigenvalue is 1.2, it means that the magnitude of the vector gets larger than the original magnitude by 20% and if the eigenvalue is 0.8, it means the vector got smaller than the original vector by 20 %. The graphical presentation of eigenvalue is as follows.
Now let's verbalize our Eigenvector and Eigenvalue definition.
Matrix multiplied to its Eigenvector is same as the Eigenvalue multiplied to its Eigenvector.
Another way to understand the meaning of the eigen vector and eigen value directly from the equation would be as follows :
Let's look into the right hand side of the equation, which is a vector x multiplied by a scalar (lamda). What does it mean ?. It mean that this is just scaling the vector and the angle of the vector does not change. It means that this part can scale the vector x but does not do any rotation to the vector. Now let's look into the left hand side of the equation A x, which is a vector multiplied by a matrix A. When you multiply a Matrix to a vector, the vector would scale in some degree, shear in some degree and rotate in some degree at the same time. But there can be a special vectors which only scales and does not do any rotation by the matrix, that specific vector (or vectors) are called eigen vector of the matrix. You can put the statement "does not do any rotation by the matrix" in another way, saying "does not change the direction of the vector". (NOTE : You need to pay attention to the meaning of 'change the direction' in this context. In reality, eigen vector can point to opposite direction of the orignal vector which is same as 180 degree rotation. But in the context of eigen value/vector, we don't call it as 'change of the direction' / 'rotation'. We call it as 'scaling by negative number'.)
What does complex number eigen value mean ?
Simply put, this mean that there is no real valued x and lamda that satisfies the following equation
As mentioned above, this equation mean as follows : there can be a special vectors which only scales and does not do any rotation by the matrix, that specific vector (or vectors) are called eigen vector of the matrix Interpreting the statement "there is no real valued x and lamda that satisfies the following equation" based on what I mentioned above, it would mean as follows. Every vectors (every points in the coordinate) gets rotated by the matrix.
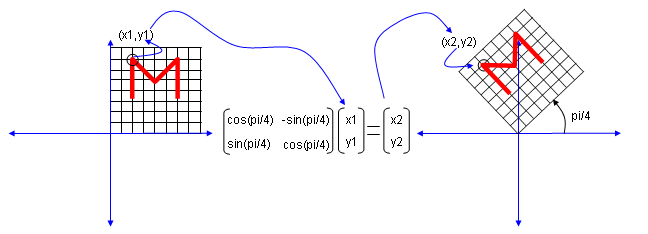
For example, let's think about a rotational matrix as shown below. this matrix rotate every point in the coordinate by pi/4 radian.
If you do the calculation of eigen value and eigen vector for this matrix, you would get complex numbered eigen value and eigen vectors as shown below.
>> M = [cos(pi/4) -sin(pi/4);sin(pi/4) cos(pi/4)]
M =
0.7071 -0.7071 0.7071 0.7071
>> [V,D,W] = eig(M)
V =
0.7071 + 0.0000i 0.7071 + 0.0000i 0.0000 - 0.7071i 0.0000 + 0.7071i
D =
0.7071 + 0.7071i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.7071 - 0.7071i
W =
-0.7071 + 0.0000i -0.7071 + 0.0000i 0.0000 + 0.7071i 0.0000 - 0.7071i
In other words, if you get the complex eigen values you can use it as the indicator that the matrix performs a rotation operation and use it as an important information about the matrix. Look into this page and see how you can utilize / interpret the complex valued eigen value/vector.
Then very important question would be "Why we need this kind of Eigenvector / Eigenvalue ?" and "When do we use Eigenvector / Eigenvalue ?".
The answer to this question cannot be done in a short word, the best way is to collect as many examples as possible to use these eigenvector/eigenvalues. You can find one example in this page, the section Geometric/Graphical Meaning of Eigenvalue and Determinant
Are Eigenvectors orthogonal to each other ?
The answer is 'Not Always'. Eigenvectors of a matrix is always orthogonal to each other only when the matrix is symmetric. One of the examples of real symmetric matrix which gives orthogonal eigen vectors is Covariance Matrix (See this page to see how the eigenvectors / eigenvalues are used for Covariance Matrix).
NOTE : compare this with Singular Value matrix in SVD(Singular Vector Decomposition). The two matrix(U and V) obtained by SVD always gives you the orthogonal vectors whereas the matrix (Q) obtained by Eigen Decomposition gives you the orthogonal vector only in special case (the special case is when the matrix is real symmetric).
Can I reconstruct the orignal matrix from eigenvectors and eigenvalues ?
If eigenvectors and eigenvalues are the fundamental characteristics of a matrix. You may think it may be possible to reconstruct a matrix from its eigenvalues and eigenvectors. Let's suppose that you have eigenvectors and eigenvalues. Using these information, you can reconstruct the original matrix as follows based on the definition of eigen decomposition. i) construct a matrix (let's call this Q) using the eigenvectors as column vectors ii) construct a diagonal matrix (let's call this S (sigma)) using eigenvectors. iii) reconstruct the orignal matrix (let's call this M) by performing Q *S * inv(Q) // '*' denote matrix multiplication.
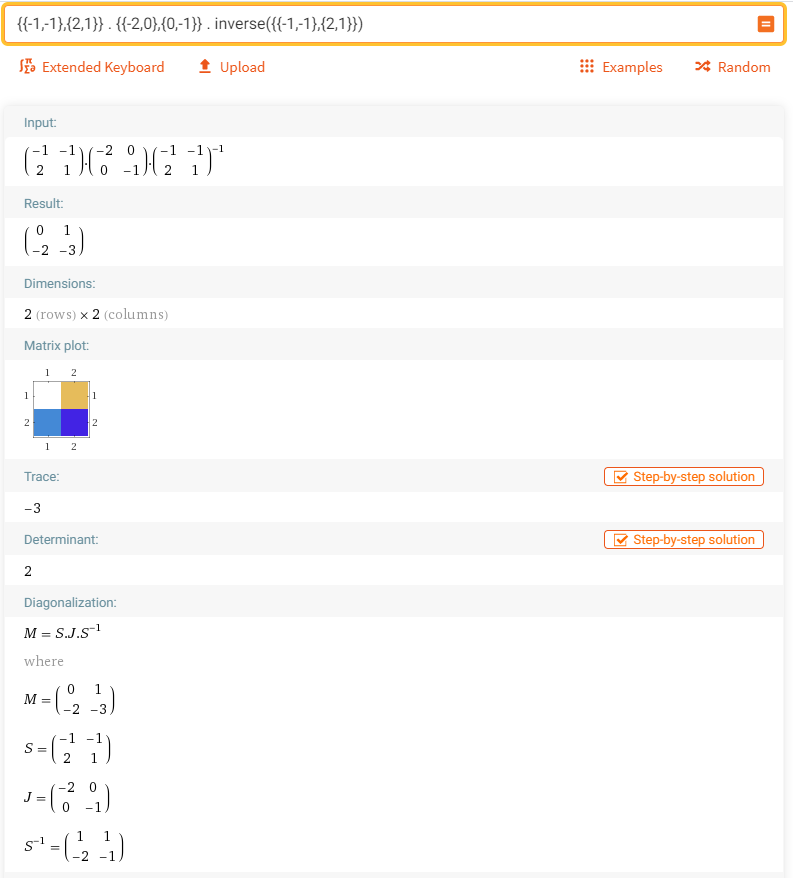
Let's take an example. I am using this example matrix from Guzinta Math/Eigenvalue Decomposition so that you can see the same thing with more diverse aspects.
Let's assume that we have two eigentvectors for a 2 x 2 matrix [-1,2] and [-1,1], and two eigen vectors -2,-1. Using these information you can construct Q and S (Q and S is the matrix mentioned the above procedure).
Q = [-1 -1 2 1]
S = [-2 0 0 -1]
Using these two matrix, you can reconstruct the original matrix M using Q *S * inv(Q). I have done this in Wolfram Alpha as shown below.
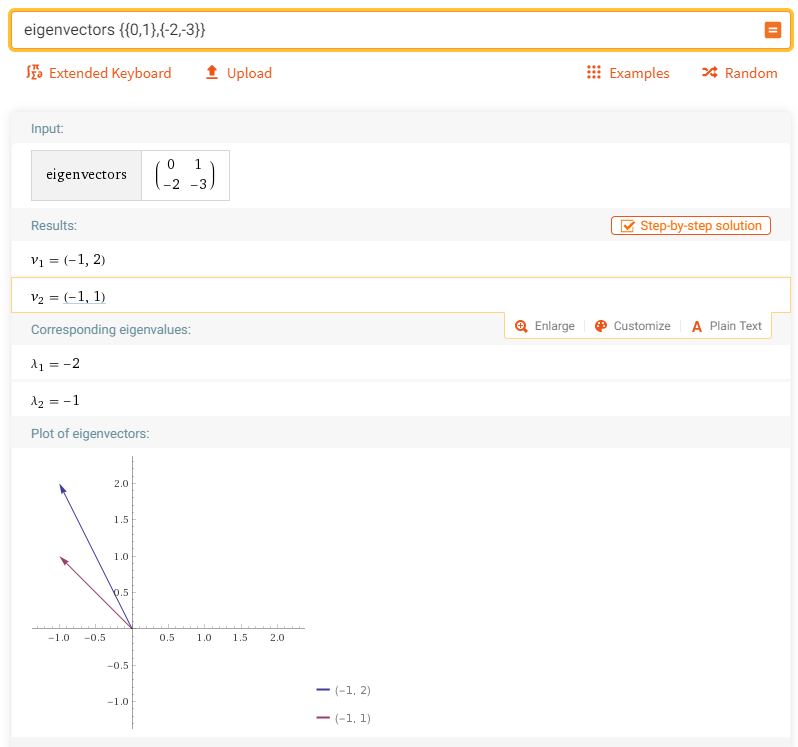
Now let's check if the reconstructed matrix produce the eigenvalues and eigenvectors same as that we used. I did this with Wolfram Alpha as shown below.
Reference :
For more examples, refer to
For useful video, try followings :
|
||