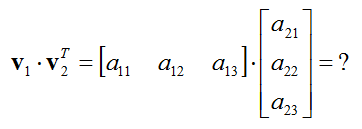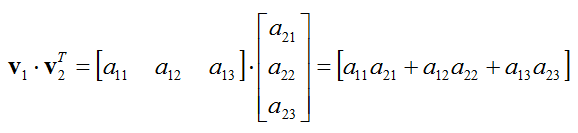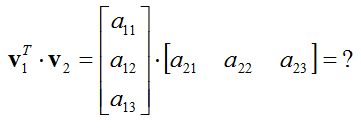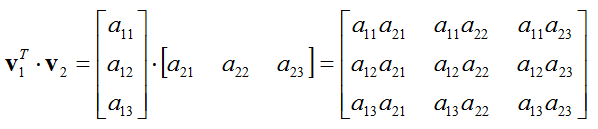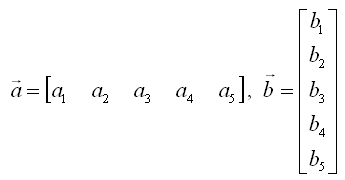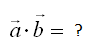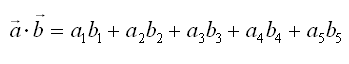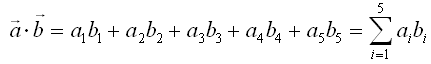Engineering Math - Matrix

  

 

 

 

Inner Product/Dot Product

 

Inner Product is a mathematical operation for two data set (basically two vector or data set) that performs following

    i) multiply two data set element-by-element

    ii) sum all the numbers obtained at step i)

This may be one of the most frequently used operation in mathematics (especially in engineering math). Sometimes it is used because the result indicates a specific mathemaatical or physical meaning and sometimes it is used just because it simplifies the mathematical representation. Anyway, it is used a LOT. Basically Innerproduct is fundamental operation for what I explains in Sum of Times (Sum of Multiplication) page.  

 

 

 

 

Geometric Meaning of Inner Product

 

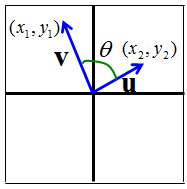
The geomatrc meaning of Inner Product is as follows. Inner Product is a kind of operation which gives you the idea of angle between the two vectors. Actually the most important application of inner product are

  • it gives the angle between the two vectors
  • it gives the degree of the correlation between two vectors

For more detailed descriptions of the application, see the last section (Applied meaning of Vector Inner Product) and read the whole pages if you are interested in how the vector inner product can indicate this kind of information.

 

  

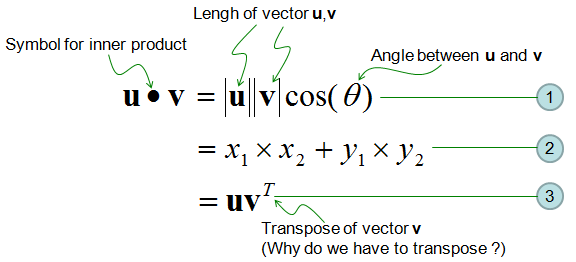
There are several different ways of representing/calculating the inner product. Equation (1) gives you the geometric meaning of inner product. Equation (2) would not shows you any idea of visualization, but it gives you a way of calculating the inner product with very simple multiplication and sums(Equation (2) would be the most common ways to calculate the inner product in most of the application). Equation (3) is the form representing the inner product as a multiplication of two vectors.

 

 

 

 

Can I do Inner Product for any two vectors ?

 

What I explained above is a kind of geometric meaning (graphical meaning) of Inner product. This kind of application can be used in 2D (two element vector) and 3D (three element vector) which can be easily visualized, but it would be difficult to interpret the inner product in this way if the number of the element grow larger. In most of the applications other than computer graphics, the inner product of vectors is done in algebric procedure as shown below.

 

As a simple example, let's think of a case of taking the inner product of two vectors which is made up of 3 elements as shown below.

 

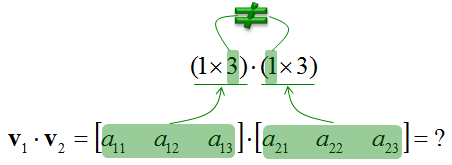
Before I ask you to take the inner product of two vectors, I would like to talk first about how to make a proper question of inner product.

First if I ask you to perform the following operation (inner product of two vectors in the following format), does it make sense to you ? Is this a valid question ?

 

 

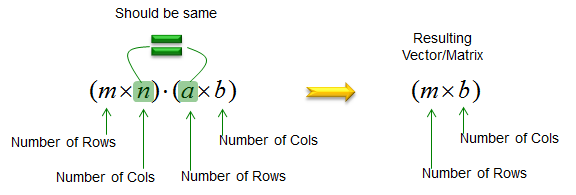
The answer is NO. The question itself is not valid. In any matrix inner product, there is an important rule as shown below (Vector is also a kind of matrix, so vector inner product should follow this rule as well. 'm x n', 'a x b', 'm x b' represents the dimension of a vector or matrix. If you are not familiar with the concept of dimension, refer to vector/matrix dimension page)

 

 

Now let's check if the problem I gave you meets this requirement. As shown below, the problem that I gave you does not meet the requirement, so the problem itself is invalid.

 

 

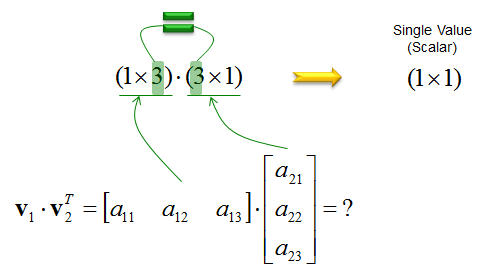
What if I change the problem as below ? (In this problem, I transposed the v2). Does this make sense ?

 

 

Yes, it make sense. It is valid problem since it meets the matrix inner product rule as shown below. One think you have to notice is that the result of this form of inner product is 1 x 1 vector. 1 x 1 vector (matrix) is same as scalar.

 

 

Now let's look how this inner product is calculated. The calculation is as simple as follows. You may have a very long calculation if the size of the vector is large. But it is just long, but it is very simple calculation. Just multiply each elements of two vectors and sum them all.

 

 

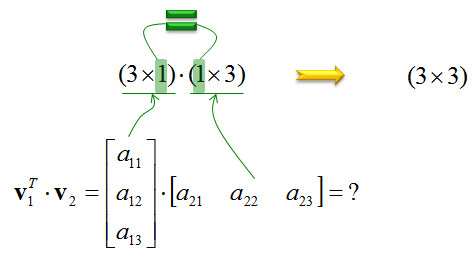
Now let's think of another example of vector porduct. This may look almost same as the previous example, but it is not exactly same. The difference is that v1 is transposed as opposed to v2 in previous example.

 

 

Before you start calculation, let's check if this problem is meaning (valid) question or not. It is valid question because it meets the inner produt rule as shown below. One important thing you need to notice in this case is that the result of the inner product in this case is 3 x 3 matrix, it is not a scalar value.

 

 

The result of calculation is as follows. I recommend you to take some time to take a close look at this.

 

 

Now let's try to increase the size of a vector and see if you can figure out the result from the simple example as explained above.

 

Let's suppose you are give two vectors as shown below.

 

And you are asked to take the inner product of the two vectors as shown below.

 

First, check if this problem itself is valid or not. (I will leave this to you. Try on your own if this problem is valid or not). Just to give you the conclusion. the answer is 'Yes, the problem is valid'.

 

What is the result of the inner product in this case ? It is going to be as follows.

 

 

If the size of vector gets very large, it would be too tedious to write the result as above. If you take a little bit closer examination of the expression, you would notice that you can simplify the expressing using 'Sum (Sigma)' notation as shown below.

 

 

 

 

Applied meaning of Vector Inner Product

 

When you see the case of vector inner product in real application, it is very important of the practical meaning of the vector inner product.

 

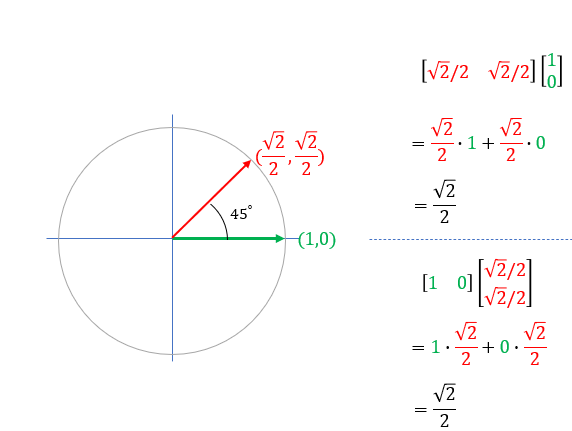
I see two major application of the inner product. One is to figure out the angle between the two vectors as illustrated above. (First, you calculate the inner product using Equation (2) and with the result and equation (1), you can figure out the angle).

This angle in turn has additional implication.  If this angle is 90 degree(0.5 pi), it means

  • the result of the inner product becomes 0
  • the correlation between the two vector is 0.
  • the two vectors are independent to each other.

If this angle is 0 degree, it means

  • the result of the inner product becomes max (multiplication of length of two vectors)
  • the correlation between the two vector is 1.
  • the two vectors are totally dependent to each other.

If this angle is between 0 and 90, the value is between min(0) and max value and they are partially dependent to each other.

 

Second application is nothing to do with geometric meaning, but it is very handy form of mathematical representation of "Sum of Multiplication/Sume of Times" as shown in "Sum of Times" page.

 

One important thing you have to remember is that the result of inner product of two vectors is a scalar.

 

 

 

Examples

 

 

Example 1 >

 

This examples shows how the angle between two vectors can be calculated by Inner Product. Click on the figure or click here for step by step process.

 

 

 

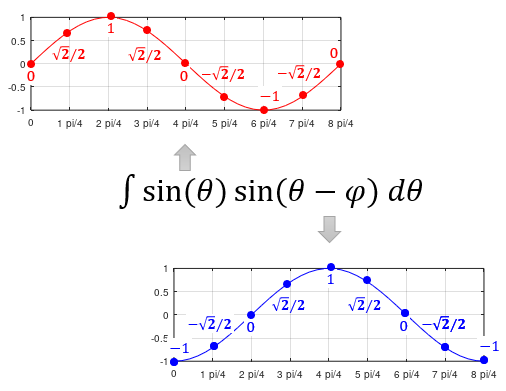
Example 2 >

 

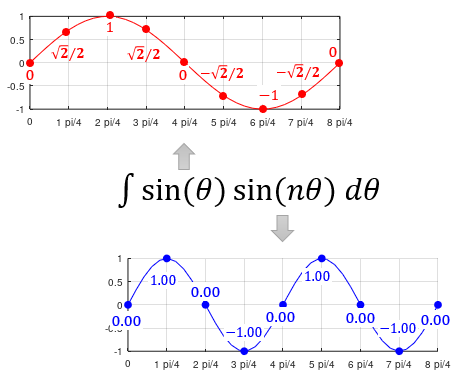
This examples shows how the inner product for the two functions can be done. Click on the figure or click here for step by step process.

 

 

 

 

Example 3 >

 

This examples shows how the inner product for the two functions can be done. Click on the figure or click here for step by step process. This type of operation is fundamental process in Discrete Fourier Transform.

 

 

 

 

Example 4 >

 

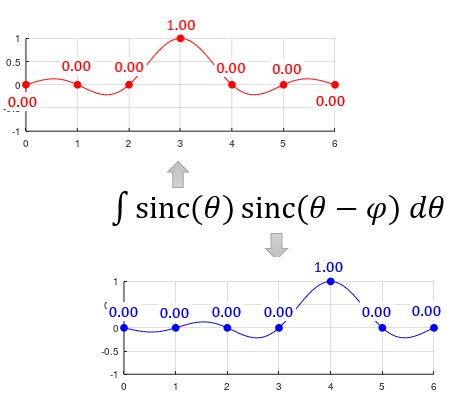
This is another that shows how the inner product for the two functions can be done. Click on the figure or click here for step by step process.

 

 

 

 

On line Calculators

 

You can find on-line calculator for your practice. it would be good for you to do calculation with pen and paper first and then check out the answer with the calculator.