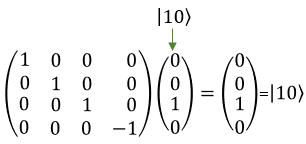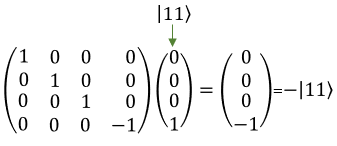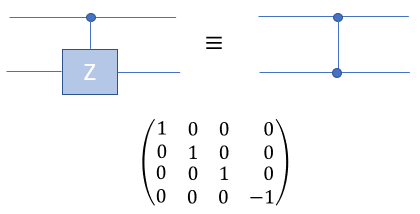
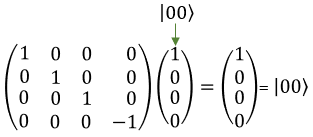
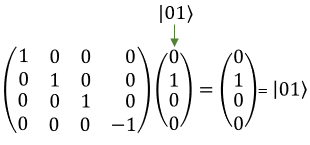
Quantum Computing

Quamtum Gate - Controlled Z

The Controlled-Z (CZ) gate is a two-qubit gate used in quantum computing. It operates on a pair of qubits, with one qubit acting as the control and the other as the target. In layman's terms, the CZ gate applies a phase flip (change in the relative phase) to the target qubit only when the control qubit is in the state |1⟩. If the control qubit is in the state |0⟩, the CZ gate does not affect the target qubit.

Here's a simple explanation of how the CZ gate works:

If the control qubit is in state |0>, the CZ gate does nothing to either qubit. They both remain in their original states.

If the control qubit is in state |1>, the CZ gate applies a phase flip (using the Pauli-Z gate) to the target qubit.

To understand the CZ gate better, let's consider its operation on the basis states of a two-qubit system:

CZ|00> = |00> (Control qubit is |0>, no change)

CZ|01> = |01> (Control qubit is |0>, no change)

CZ|10> = |10> (Control qubit is |1>, no change to target qubit |0>)

CZ|11> = -|11> (Control qubit is |1>, phase flip applied to target qubit |1>)

In the case of the CZ gate applied to qubits in superposition, let's consider the action on the following two-qubit state:

|ψ> = a|00> + b|01> + c|10> + d|11> where a, b, c, and d are complex coefficients.

When the CZ gate is applied to this state, the result will be:

CZ|ψ> = a|00> + b|01> + c|10> - d|11>

As you can see, the CZ gate has applied a phase flip to the amplitude of the |11> state, while the other states remain unchanged.

In symbol and mathematical form, it is presented as follows. It takes 1 bit as input and return 1 bit as output. If you look into the matrix form, you would notice that it takes 4x1 vector (representing 2 qubit) and swap the elements within the vector.

If I you plug in the state vector for |00> , |01>, |10> and  |11> into T gate matrix equation, you can get the output as follows. You would see that the element in the statevector get swaped by the gate T matrix.