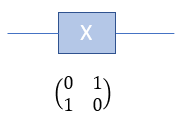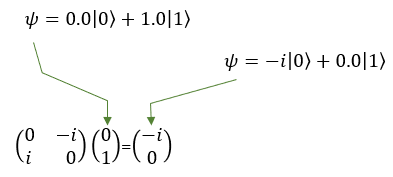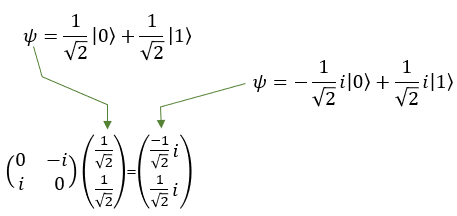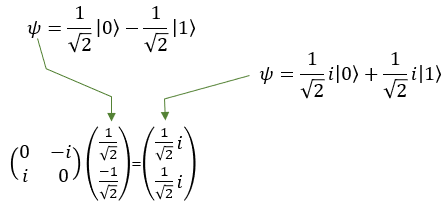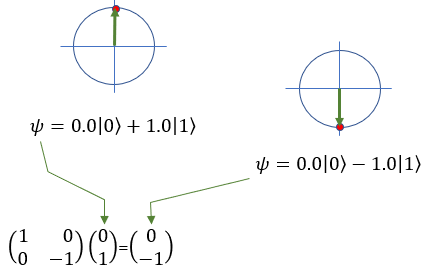|
|
|||||||||||||
|
The Pauli gates are a set of one-qubit operations that play a fundamental role in the manipulation of quantum states. There are three Pauli gates, represented by the Pauli matrices: X, Y, and Z. These gates are essential building blocks for more complex quantum circuits and algorithms. They allow for state manipulation and provide the foundation for the implementation of larger quantum operations. There are three gates that belong to Pauli gates :
In the context of quantum computing, a flip and a phase flip refer to different types of transformations applied to qubit states. A flip, also known as a bit-flip, is a transformation that changes the state of a qubit from |0> to |1> or from |1> to |0>, just like a classical NOT gate changes the state of a classical bit from 0 to 1 or 1 to 0. The Pauli-X gate performs this flip operation on qubits. When applied to a qubit, the Pauli-X gate essentially swaps the amplitudes of the |0> and |1> states. For example: X |0> = |1> X |1> = |0>
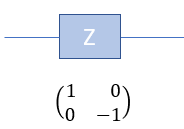
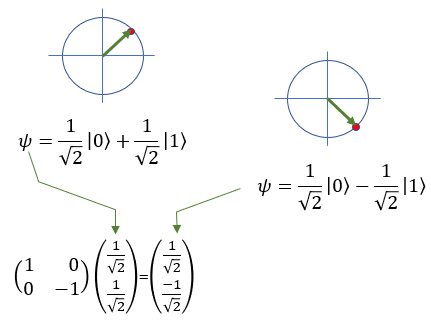
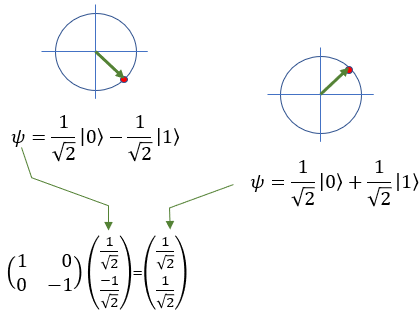
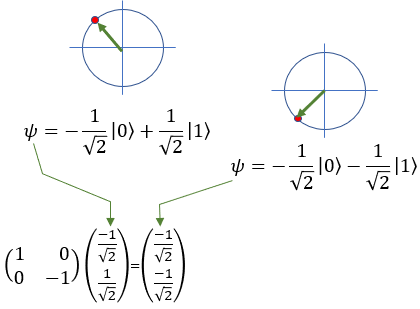
A phase flip is a transformation that changes the relative phase of the |1> state while leaving the |0> state unchanged. In this case, only the phase of the qubit state changes, not the actual basis states themselves. The Pauli-Z gate is responsible for phase flips. When applied to a qubit, the Pauli-Z gate changes the sign of the amplitude of the |1> state, while the amplitude of the |0> state remains the same. For example: Z |0> = |0> Z |1> = -|1> Following is the type of flip operation for X, Y, Z gate
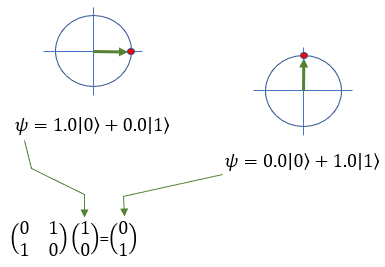
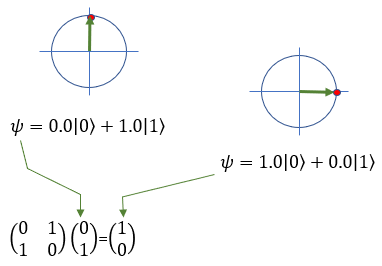
Quamtum Gate - X (Pauli-X)The Pauli-X gate is also known as the bit-flip gate and works on a single qubit. Pauli-X gate acts like a "quantum NOT gate." A classical NOT gate inverts a binary bit, changing 0 to 1 and 1 to 0. Similarly, the Pauli-X gate flips a qubit's state, switching |0⟩ to |1⟩ and |1⟩ to |0⟩. Here's an example: If you have a qubit in the state |0⟩ and apply the Pauli-X gate, the qubit's state changes to |1>. If you have a qubit in the state |1⟩ and apply the Pauli-X gate, the qubit's state changes to |0>. However, since qubits can exist in superpositions, the Pauli-X gate can also transform states that are combinations of |0> and |1>. For example, consider a qubit in the following superposition state: |ψ> = a|0> + b|1>, where a and b are complex numbers representing the amplitudes of the qubit states. When the Pauli-X gate is applied to this qubit, the result will be: X|ψ> = a|1> + b|0> As you can see, the Pauli-X gate has effectively swapped the amplitudes of the |0> and |1> states. In symbol and mathematical form, it is presented as follows. It takes 1 bit as input and return 1 bit as output. If you look into the matrix form, you would notice that it takes 2x1 vector (representing 1 qubit) and swap the elements within the vector.
If I you plug in the state vector for |0> and |1> into X gate matrix equation, you can get the output as follows. You would see that the element in the statevector get swaped by the gate X matrix.
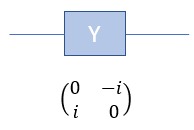
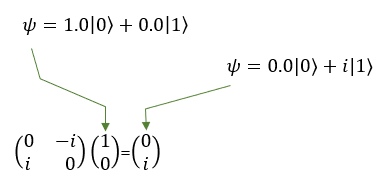
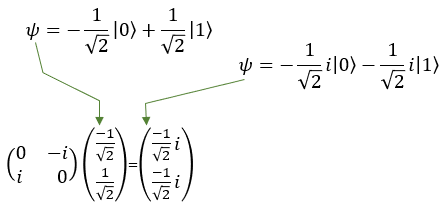
Quamtum Gate - Y (Pauli-Y)The Pauli-Y gate is another fundamental operation in quantum computing, acting on a single qubit. The Pauli-Y gate is a combination of the Pauli-X and Pauli-Z gates, meaning it applies both a bit-flip and a phase-flip to the qubit. It mean that the Pauli-Y gate not only changes the state of the qubit (like the Pauli-X gate), but it also changes the relative phase between the states |0> and |1> (like the Pauli-Z gate). For example, if you have a qubit in the state |0> and apply the Pauli-Y gate, the qubit's state changes to the state i|1> , where i is the imaginary unit (i^2 = -1). If you have a qubit in the state |1⟩ and apply the Pauli-Y gate, the qubit's state changes to the state -i|0>. However, since qubits can exist in superpositions, the Pauli-Y gate can also transform states that are combinations of |0> and |1>. For example, consider a qubit in the following superposition state: |ψ> = a|0> + b|1>, where a and b are complex numbers representing the amplitudes of the qubit states. When the Pauli-Y gate is applied to this qubit, the result will be: Y|ψ> = -i b|0> + i a|1> As you can see, the Pauli-Y gate has not only swapped the amplitudes of the |0> and |1> states but also added a relative phase of i to the resulting states. In symbol and mathematical form, it is presented as follows. It takes 1 bit as input and return 1 bit as output. If you look into the matrix form, you would notice that it takes 2x1 vector (representing 1 qubit) and swap the elements within the vector.
If I you plug in the state vector for |0> and |1> into Y gate matrix equation, you can get the output as follows. You would see that the element in the statevector get swaped by the gate Y matrix.
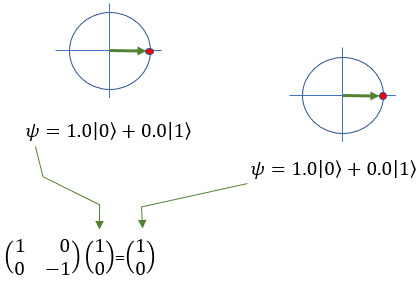
Quamtum Gate - Z (Pauli-Z)The Pauli-Z gate is also known as the phase-flip gate working on a single qubit. Unlike the Pauli-X gate, which flips the state of a qubit (acting like a "quantum NOT gate"), the Pauli-Z gate changes the relative phase between the states |0> and |1>, without changing the basis states themselves. In layman's terms, the Pauli-Z gate modifies the "phase" of the qubit's state, which is an essential aspect of quantum mechanics. For example, if you have a qubit in the state |0> and apply the Pauli-Z gate, the qubit's state remains unchanged, staying in the state |0>. If you have a qubit in the state |1> and apply the Pauli-Z gate, the qubit's state changes to the state -|1>, which means the relative phase between the |0> and |1> states has been inverted. Since qubits can exist in superpositions, the Pauli-Z gate can also transform states that are combinations of |0> and |1>. For example, consider a qubit in the following superposition state: |ψ> = a|0> + b|1>, where a and b are complex numbers representing the amplitudes of the qubit states. When the Pauli-Z gate is applied to this qubit, the result will be: Z|ψ> = a|0⟩ - b|1> As you can see, the Pauli-Z gate has changed the sign of the amplitude of the |1> state, while the amplitude of the |0⟩ state remains the same. In symbol and mathematical form, it is presented as follows. It takes 1 bit as input and return 1 bit as output. If you look into the matrix form, you would notice that it takes 2x1 vector (representing 1 qubit) and swap the elements within the vector.
If I you plug in the state vector for |0> and |1> into Z gate matrix equation, you can get the output as follows. You would see that the element in the statevector get swaped by the gate Z matrix.
|
|||||||||||||