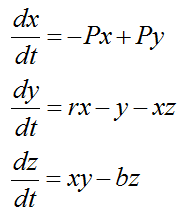The Lorenz attractor is one of the most iconic visualizations in chaos theory, illustrating how deterministic systems - those governed by precise laws - can nonetheless exhibit unpredictable and seemingly random behavior. It was first discovered by Edward Lorenz, a meteorologist, in 1963 while studying simplified equations to model atmospheric convection. He developed a system of three coupled, non-linear differential equations to describe the motion of fluid under certain thermal conditions. These equations track how three variables - commonly denoted as x(t) (convection rate), y(t) (horizontal temperature variation), and z(t) (vertical temperature variation) - evolve over time.

Despite their simplicity, the Lorenz equations exhibit sensitive dependence on initial conditions, a hallmark of chaotic systems. This means that even a minute change in starting values can lead to drastically different outcomes over time. This sensitivity is often metaphorically captured by the phrase "the butterfly effect," suggesting that the flap of a butterfly’s wings in Brazil could set off a tornado in Texas.

Graphically, the Lorenz attractor forms a strange attractor - a fractal structure in 3D space that resembles the shape of butterfly wings. Rather than converging to a fixed point or a periodic orbit, the trajectories of the system spiral indefinitely around two focal points, never repeating and never escaping. This shows how deterministic rules can lead to long-term unpredictability, blurring the line between order and chaos.

The Lorenz attractor has since become a foundational model not just in meteorology, but in a wide range of disciplines—from fluid dynamics and engineering to biology, neuroscience, and even economics - where complex, dynamic systems are studied. It reminds us that complexity does not always require complexity in laws, but can emerge from the recursive interaction of simple rules.

Build up Intuition

Before diving into the mathematical intricacies of the Lorenz system, it's helpful to first develop an intuitive understanding of how the system behaves and what role each parameter plays. One effective way to do this is by interacting with a simple simulation program that visualizes the system's evolution over time. By observing how the system responds to changes in parameters, you can gain a hands-on feel for the dynamics at play. This approach makes it easier to grasp the deeper concepts behind the equations, and it bridges the gap between abstract mathematics and real-world behavior. Instead of jumping straight into theory, let’s first explore how simple tweaks in the parameters influence the overall pattern and motion - this will build a strong foundation for understanding the fascinating chaotic behavior that follows.

The system is described by three coupled differential equations:

dx/dt = σ(y - x)

dy/dt = x(ρ - z) - y

dz/dt = xy - βz

Where:

• σ (sigma) is the Prandtl number, representing the ratio of kinematic viscosity to thermal diffusivity
• ρ (rho) is the Rayleigh number, related to the temperature difference between the top and bottom of the system
• β (beta) is a geometric factor related to the size of the system

This is the usage of this program.

Parameters Control

• Sigma (σ): Controls the rate of convection (default: 10)
• Rho (ρ): Controls the temperature difference (default: 28)
• Beta (β): Controls the ratio of box dimensions (default: 2.67)

Initial Conditions

• X0: Initial X coordinate (default: 0.1)
• Y0: Initial Y coordinate (default: 0)
• Z0: Initial Z coordinate (default: 0)

Visualization Options

• Color Scheme: Choose between Rainbow, Fire, Ocean, and Grayscale
• Time Step: Adjust simulation speed (0.001 to 0.05)
• WebGL Toggle: Enable/disable WebGL rendering

Camera Controls

• Left Mouse: Rotate view
• Right Mouse: Pan view
• Mouse Wheel: Zoom in/out
• Reset View: Return camera to default position

Actions

• Start/Pause: Toggle simulation
• Reset: Clear and restart simulation
• Save Image: Capture current view as image

How it works ?

Lorenz attractor is obtained by solving a system of non-linear differential equation numerically as shown below. If you plot the solution of each single variable (fuction) on time domain (i.e, x(t), y(t), z(t)) you would see a pretty much radom like plots, but if you plot any of the two variables (or 3 variables) in parametric plot, you would see some pattern as shown below. The exact trajectory for each function(variable) changes very unpredictable way as you change the initial value by even very small degree, you would still see very similar overall plot. This is why the solution of the system equation is called as an attractor.

Here, P, r, and b are parameters that define the behavior of the system, such as the Prandtl number, Rayleigh number, and a geometric factor. The parameters shown in this equation maps to the parameters shown in the program in previous section as follows

• P = sigma
• r = Rho
• b = Beta

Physical Interpretation of the Parameters

Understanding the physical interpretation of the parameters in the Lorenz system is essential for grasping how this seemingly simple model gives rise to chaotic behavior. Each parameter—sigma (σ), rho (ρ), and beta (β)—has a concrete meaning rooted in fluid dynamics and thermodynamics. These constants are not arbitrary; they represent specific physical properties of the system such as the ratio of momentum to thermal diffusion, the strength of buoyancy-driven convection, and geometric characteristics of the environment. By examining how these parameters influence the evolution of the system’s variables, we gain deeper insight into the mechanisms that drive instability, feedback loops, and ultimately, the emergence of chaos.

σ (Sigma) – Prandtl Number

Definition:

σ = ν / α

where:

ν is the kinematic viscosity (momentum diffusivity)

α is the thermal diffusivity (heat diffusivity)

Physical Meaning:

• Sigma (σ) measures the relative effectiveness of momentum diffusion compared to heat diffusion.
• It reflects how quickly velocity changes (due to viscosity) spread out compared to temperature changes.

Interpretation:

• Low σ → thermal diffusion dominates (heat spreads faster than momentum)
• High σ → momentum diffuses more efficiently than heat
• A common value used in simulations is σ = 10.

Effect on the Lorenz System:

σ controls the coupling between the x and y variables, influencing how rapidly the fluid responds to thermal gradients with motion.

ρ (Rho) – Rayleigh Number

Definition:

ρ = (g β_T ΔT d³) / (ν α)

where:

• g is gravitational acceleration
• β_T is the thermal expansion coefficient
• ΔT is the temperature difference between the top and bottom
• d is the depth of the fluid layer
• ν is kinematic viscosity
• α is thermal diffusivity

Physical Meaning:

• Rho (ρ) quantifies the intensity of thermal forcing relative to damping effects.
• It measures how strongly buoyancy drives convection in the system.

Interpretation:

• Low ρ → no convection
• Critical ρ → convection starts
• High ρ → turbulence or chaos develops

Effect on the Lorenz System:

ρ determines the transition from stable to chaotic behavior, controlling the strength of instability in the system.

β (Beta) – Geometric Factor

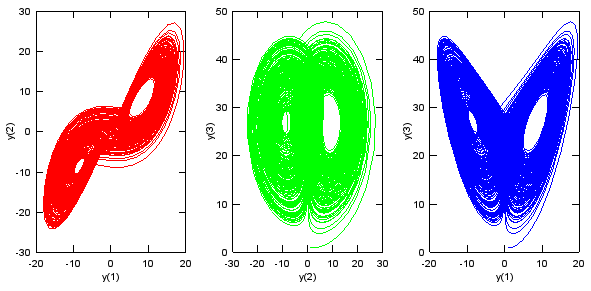
Definition:

β = 4 / (1 + a²)

where a is a system-specific geometric ratio (e.g., aspect ratio of convection cells)

Physical Meaning:

Beta (β) reflects the vertical structure of the system, specifically how vertical temperature gradients influence motion.

Interpretation:

• Large β → stronger damping of vertical fluctuations
• Small β → slower decay, more vertical variability

Effect on the Lorenz System:

β influences how quickly the z variable (vertical temperature deviation) evolves and stabilizes.

Numerical Solution of the Equation

When solved numerically, the solutions to these equations - x(t), y(t), and z(t) - appear random when plotted individually over time. However, when plotted in a parametric space (e.g., plotting x versus y, y versus z, or x versus z), the solutions reveal a fascinating and intricate pattern. This pattern, known as the Lorenz attractor, has a characteristic butterfly shape and is deterministic yet highly sensitive to initial conditions.

This sensitivity means that even a minuscule change in the initial values of x, y, or z leads to vastly different trajectories over time, a hallmark of chaotic systems. Despite this unpredictability in the exact trajectories, the overall structure of the attractor remains consistent. This robustness is why the Lorenz attractor is called an "attractor": it "attracts" the system's state into a specific, complex pattern that persists over time, regardless of small perturbations in the starting conditions.

The Lorenz attractor is widely studied because it beautifully demonstrates the principles of chaos theory, such as deterministic chaos and the underlying order within seemingly random systems. It also has practical implications in meteorology, engineering, and physics, as it highlights the challenges of long-term prediction in systems with chaotic behavior.

The solution of the equation are plotted as below.

The Matlab code to get the solution to the equations and plot them is as follows :

%Save the following contents in a .m file and run the .m file

% this is tested only in Matlab, not in Octave

P = 10;

r = 28;

b = 8/3;

 

dy_dt = @(t,y) [-P*y(1)+P*y(2);...

                    r.*y(1)-y(2)-y(1)*y(3);...

                    y(1)*y(2)-b.*y(3)];

 

odeopt = odeset ('RelTol', 0.00001, 'AbsTol', 0.00001,'InitialStep',0.5,'MaxStep',0.5);

[t,y] = ode45(dy_dt,[0 250], [1.0 1.0 1.0],odeopt);

 

subplot(1,3,1);plot(y(:,1),y(:,2),'r-'); xlabel('y(1)'); ylabel('y(2)');

subplot(1,3,2);plot(y(:,2),y(:,3),'g-'); xlabel('y(2)'); ylabel('y(3)');

subplot(1,3,3);plot(y(:,1),y(:,3),'b-'); xlabel('y(1)'); ylabel('y(3)');