Communication Technology

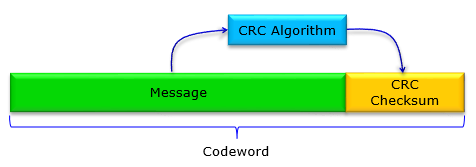
CRC(Cyclic Redundancy Checksum)

CRC is a kind of Error Check technology and stands for Cyclic Redundancy Checksum. The way it is used can be illustrated as follows. More detailed explanation about the concept and application of CRC is described in CRC in Error Check page. However, I decided to create a separate page for this topic mainly to deal with some examples in very detail. I want to explain on these examples in more practical way rather than too much theoretical way (If you are interested in the theoretical background, you can look into 'division of polynomial in Galois Field 2').

Example 1 >

This example itself came from an example in Ref [1]. However, the way I explain on this would be pretty much different from the ref [1] or most of textbooks. I tried to write down every steps as I am calculating the checksum by hand.

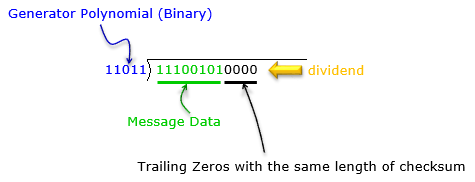
Most of the CRC problems are given as follows. You will be given a generator polynomial and a message data from which you need to calculate the checksum bits

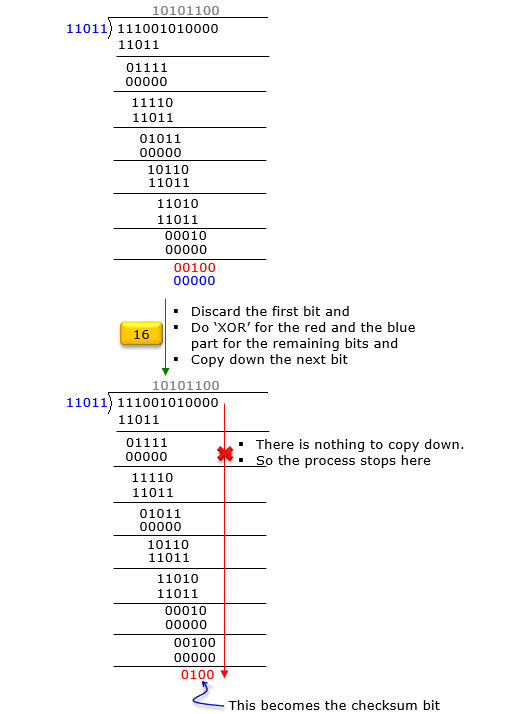
Before you jump into solving the problem, let's rewrite the given information into a little bit different format (as in red)

Once you get these information, build a binary division equation as follows (as you see, the dividend is created by combining the given message data and trailing zeros.

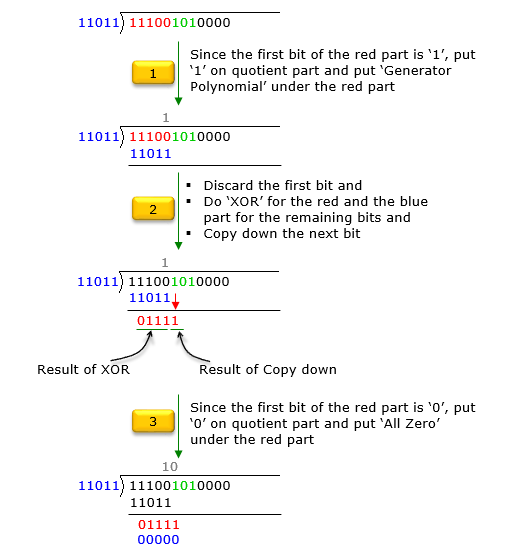
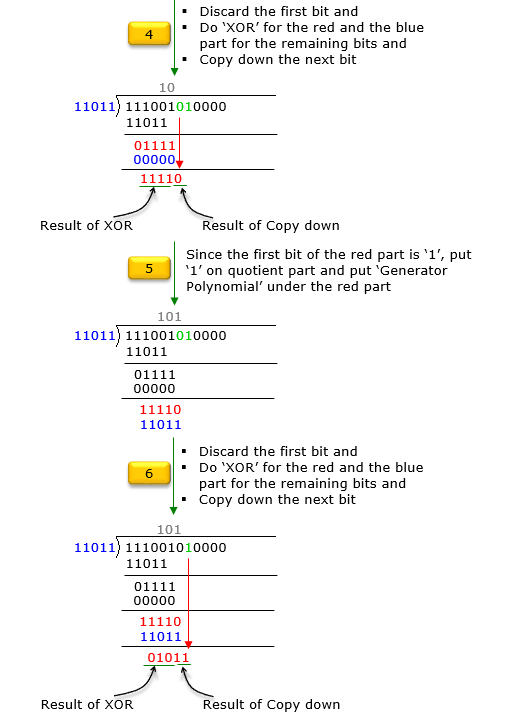
If you are familiar with binary operation (GF(2) polynomial division), just drawing the equation above would be enough and you may directly write down the solution as follows.

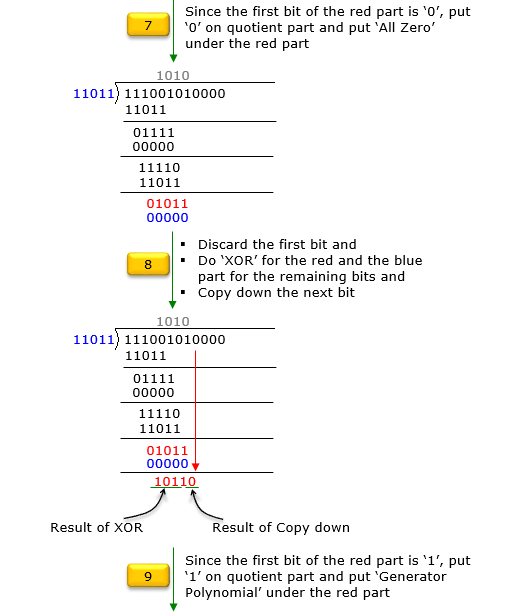
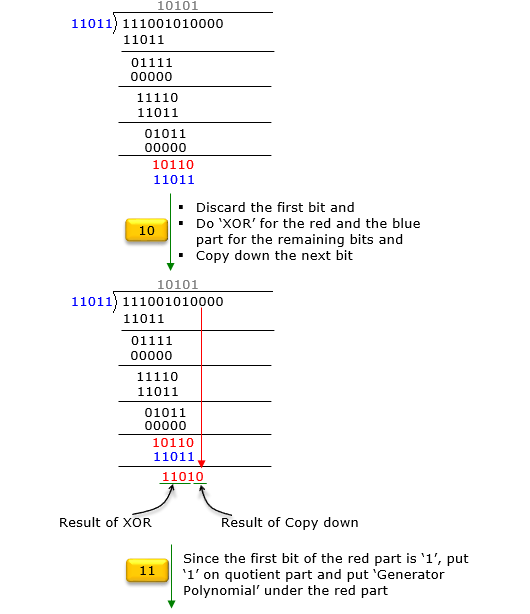
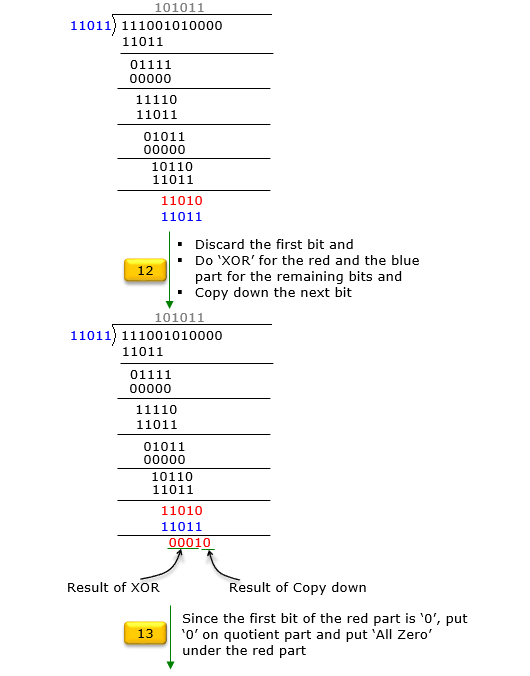
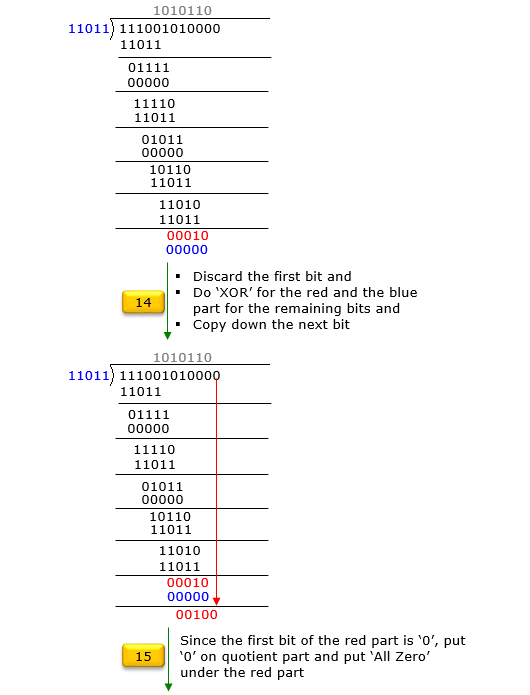
If you are not familiar with the GF2 division or you want to have the solution process in more like computer algorithm rather than mathematical formula, go through following steps. Just reading through these steps may confuse you. I would suggest you write down each and every steps shown here by paper and pencil.

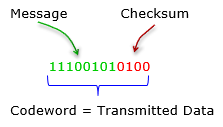
With the checksum that was calculated above and the message data, you can create the codeword that is to be transmitted.

Reference :

[1]  CRC Series, Part 3: CRC Implementation Code in C/C++