DE - Modeling Home : www.sharetechnote.com
How to determine the component equation ?
This page is intended as a supplimentary page to Coupled Springs : Two coupled spring without Damping but this page will be helpful with almost all examples introduced in the Spring Mass model page. However, this page is not about deriving the whole set of differential equations for a system. This page would focus on only one thing... it is about how to determine the 'sign' of the each terms (components) in the equation. In some differential equation, determining the sign of the component is pretty simple and obvious. For example, if you are modeling a mixing tank where some fluid flowing into it and some fluid following out of the tank. In this case, you can simply put '+' for the fluid flowing into the tank and put '-' for the fuild flowing out of the tank. However, in some physical system.. especially the physical model based on the displacement of objects. The situation gets even more complicated if the multiple objects are linked together and the objects are allowed to move in multiple direction. Determining the sign of each components of the differential equation is extremely complicated and confusing.
In this page, I will use one sample system which is comprised of two objects connected with three springs as shown below. I will show how the sign of each mathematical components (marked in red shade). Even though I will try to visualize it as much as possible, it would not be obvious and clear to you if you don't pay extremely strong attention to it. If possible, I strongly recommend you to draw all the diagram on your own on paper and put the comments on your own words.
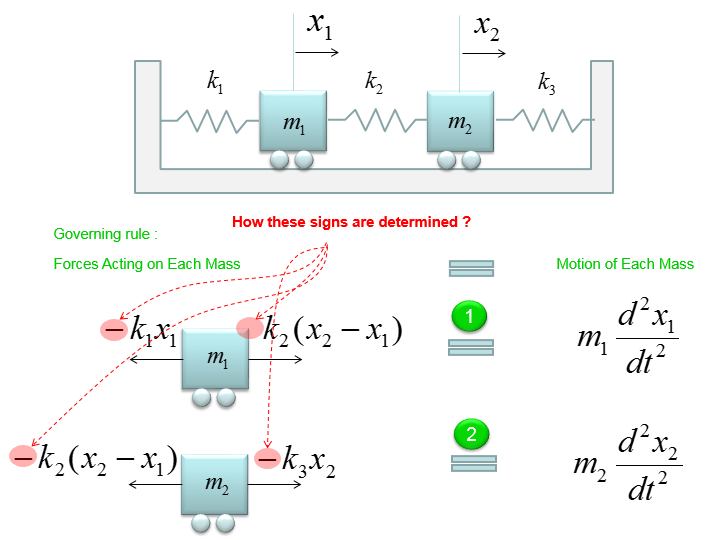
The first step (the most important step) is to devide a system into multiple building blocks. In this example, I will devide the system with reference to two mass. Since this model has two mass, you can easily guess that this system will generate two differential equations. Also, you can easily guess that the force exerting on each mass would have two components since each of the mass is allowed to move only in two directions (left and right).
Based on this big picture, let's devide the system according to each of the mass and its component force.
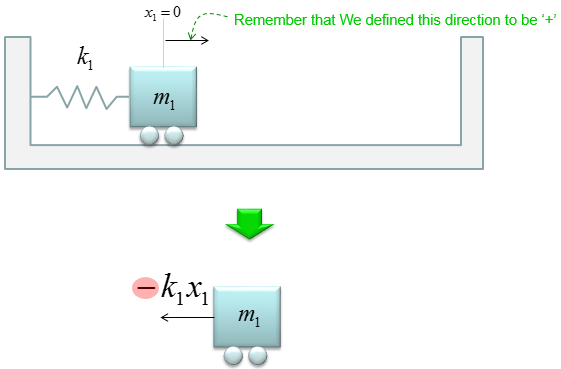
The first component can be illustrated as below. This shows only mass 1 (m1) and the force generated by the spring on the left side. At this step, one of the most important thing is to determine the reference direction. It means 'determning which direction will be marked as '+' and which direction will be marked as '-'. You can determine as you like, but depending on how you determine this reference direction, the 'sign' for each mathematical component will be different. So, once you determine the reference direction you have to apply the rule consistently.
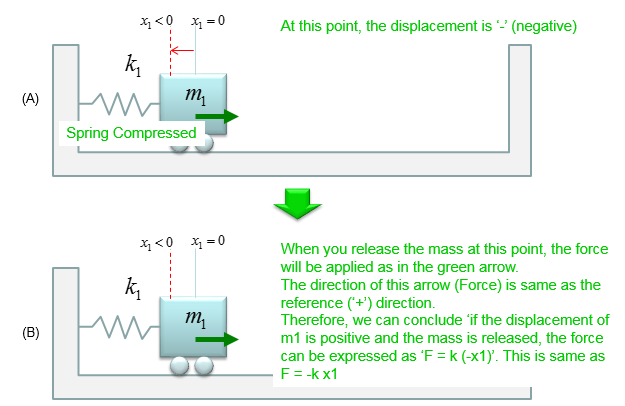
In this example, I will set 'the direction to the right' to be '+' as marked below (Actually it is a kind of convention to set the reference this way). Then, the force generated by the spring k1 is expressed as shown below.
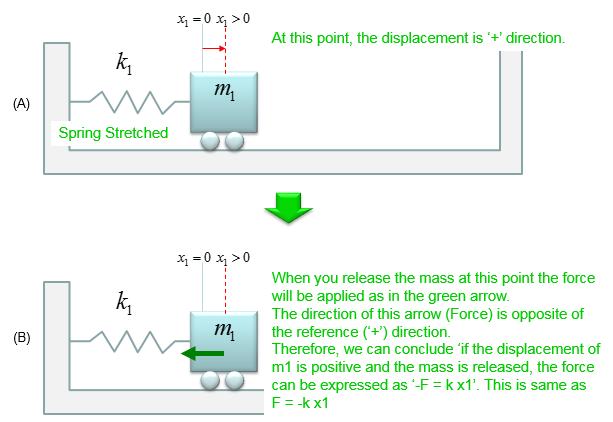
Now you may ask 'Why this component has negative sign (-) ?'. For this, you have to think of all the possible cases of displacement of m1. Let's think of the case where the initial displacement of m1 is in positive location (i.e, a point to the right from the reference point as shown below). In this case, the force generated by the spring k1 will be as shown below. You will notice that the term gets '-' sign regardless of the initial displacement of m1.
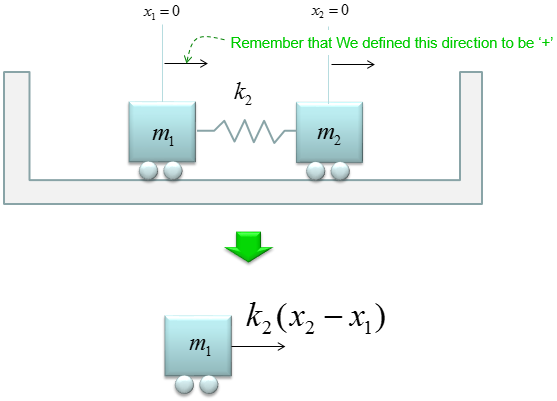
Now let's look at the right side of the component m1. This shows only mass 1 (m1) and the force generated by the spring on the right side. In this case, m2 is included as a part of modeling m1. This is because the location of m2 influence the state of k2. That is, only the position of m2 is used in this component. Mass of m2 is not included in this model. The mathematical component in this part is shown below.
As you see here, you don't see the negative sign in this component. It means this component has '+' sign with it. In this part, you have to think of a lot of different cases to confirm about the sign. But I will show you only two cases here.
The first case is where the initial displacement of m1 and m2 are both in positive location, but the displacement of m2 is greater than the displacement of m1. So the sign of (x2-x1) become positive. In this case, the force exerted on m1 become as described below. Notice the sign of the component become '+'.
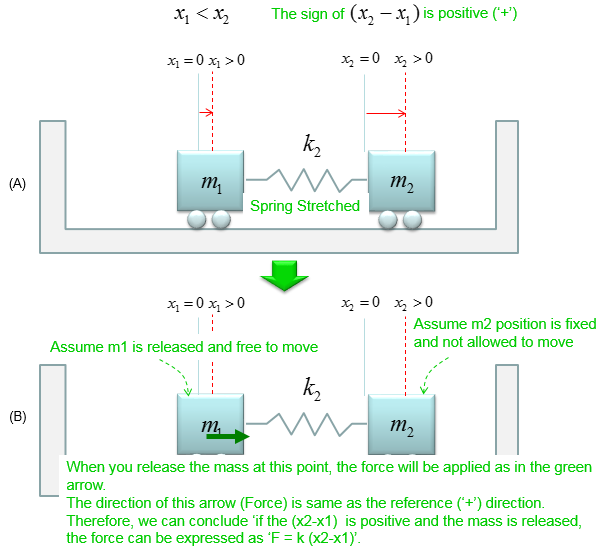
Now let's look at another case is where the initial displacement of m1 and m2 are both in positive location, but the displacement of m2 is smaller than the displacement of m1. So the sign of (x2-x1) become negative. In this case, the force exerted on m1 become as described below. Notice the sign of the component become '+' as well. It means regardless of the magnitude of x1 and x2, this component will always have '+' sign with it.

Now let's look at the force around m2. But I would not draw all the cases as above (I am a little tired now and my brain got saturated :). I will add the diagram for each case next time when I have time.. but I strongly recommend you to draw each case of the diagram on your own as I did above).
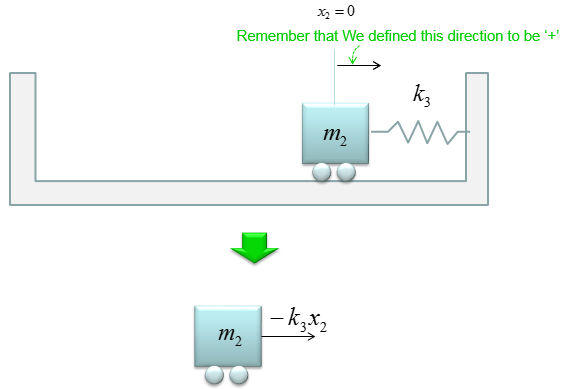
First, think of the case of forces exerting on m2 by the spring on the left side of m2. The model and mathematical model is as shown below. As you see here, this component has negative sign(-) with it.
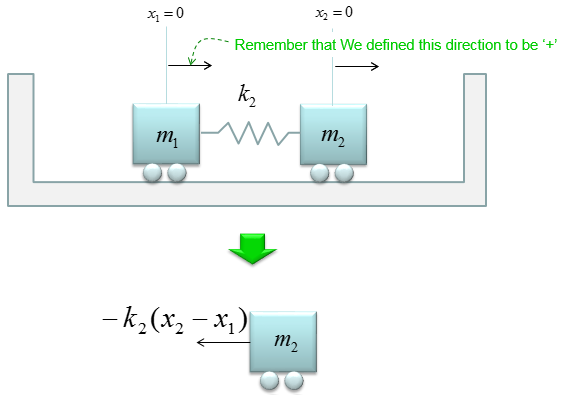
Now, think of the case of forces exerting on m2 by the spring on the right side of m2. The model and mathematical model is as shown below. As you see here, this component has negative sign(-) with it.