|
|
||
|
Time Sync ProcessAt very high level, the process of Timing Synchronization can be described as follows.
This Sync detection is done every 5 ms. (You will understand this time interval if you look at the LTE Downlink frame structure explained at DL FrameStructure section) As I mentioned in previous section, three different sequences are used as the primary sync signal and there is a one-to-one mapping between each of the three sequences and the cell ID within the cell identity group. After a UE detect this cell-identity group, it can determine the frame timing. From this cell identity group, the UE also figure out which pseudo-random sequence is used for generating the reference signal in the cell.
If you go into a little bit further details, you would need a couple of additional steps as follows (step (1) and step (2)). To detect PSS and SSS, you need to get the data with a sequence of specific resource elements accurately. To accurately extract the data from a specific resource elements, you need to know the exact symbol boundary (starting sample and ending sample of an OFDM symbol). Once you detect the exact symbol boundary, you can detect the frequency offset (a kind of frequency error) to further compenstate the signal. In some sense, these two steps are more difficult than PSS, SSS detection.
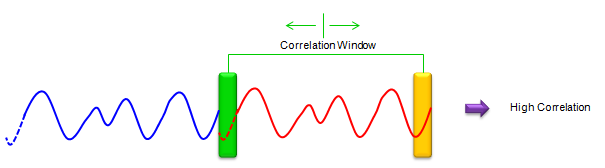
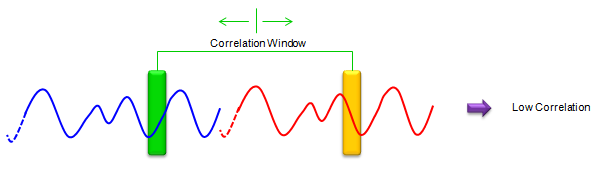
You may use different techniques for detecting the symbol boundary, but one of the common techniques being used is to use the property of Cyclic prefix. As you know, Cyclic Prefix is a copy of a sequence of data from the ending part of an OFDM symbol. It means that the correlation between a cyclic prefix and the ending part of a symbol should be very large comparing to other region as illustracted below.
< Fig 1 : a case when the correlation window is located exactly in Cyclic Prefix and the ending part of the symbol >
<Fig 2 : a case when the correlation window is not at the position of Cyclic Prefix and the ending part of the symbol> Using this properly, if you find the point where you get the highest correlation while you are sliding down the two correlation windows along the captured time domain data. You can find the symbol boundary. Following is an example of plotting these correlations while sliding the windows sample by sample. You can obviously see the peaks with the interval of one OFDM Symbol (this is from the 5 Mhz BW LTE Downlink data sampled at 7.62 Mhz sampling rate).
So far so good ? Sound simple ? Maybe. But nothing goes like textbook in real engineering. Even though the cyclic prefix should be identical to the ending part of a symbol, in reality it would not be exactly same because different noise (or fading) has been applied while the signal is generated and travels through the signal path. So the correlation peak may now show up exactly at the expected point. Also the peak value may not be at only one point.. you may see similar high correlation around several samples around the peak. So you would have some errors of the location of the peaks in several samples. The accuracy of these correlation peak would be more accurate as the length of correlation window gets longer. It means you may have pretty good accuracy in wider bandwidth because CP length is longer in wider bandwidth. However, the accuracy of the correlation gets poorer as system bandwidth gets narrower since CP length gets shorter. Therefore, in real implementation, you would need some additional tricks to compensate this kind of errors. Reference :[1] 3GPP TS 36.211 Physical Channel and Modulation [2] Jung-In Kim et al, SSS Detection Method for Initial Cell Search in 3GPP LTE FDD/TDD Dual Mode Receiver [3] Synchronization and Cell Search [4] An improved Synchronization signal detection algorithm in LTE 230 [5] Design and Analysis of an Efficient Primary Synchronization Signal Detector [6] Cell Search and Uplink Synchronization in LTE
|
||